January Labor-Market Update

US labor-market numbers for January 2024 are in. The labor market remains inefficiently tight—in fact it tightened very slightly since December.

The US labor-market numbers for January 2024 just came out. This post uses the latest numbers on vacant jobs and unemployed workers from the Bureau of Labor Statistics to compute three key statistics:

• Labor-market tightness

• Efficient unemployment rate

• Unemployment gap

The US labor market is broadly in the same situation as in December 2023, just slightly tighter. So the labor market remains inefficiently tight. The Beveridge curve shifted a little outwards, raising the efficient unemployment rate very slightly to 4.5%.

New developments

The US labor-market statistics for January 2024 are as follows:

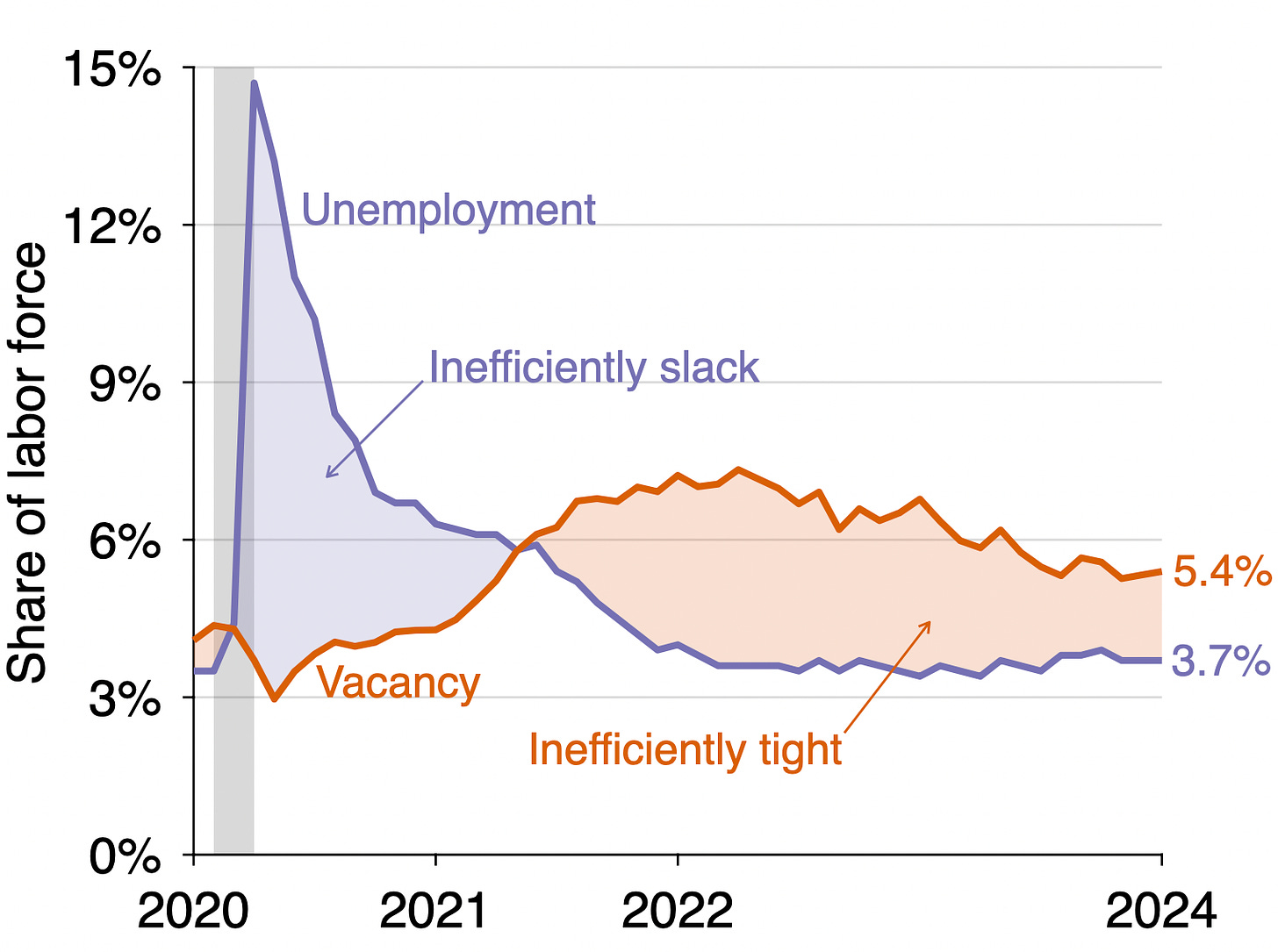
• Unemployment rate: u = 3.7%. This is the same as in December

• Vacancy rate: v = 5.4%. This is up from 5.3% in December.

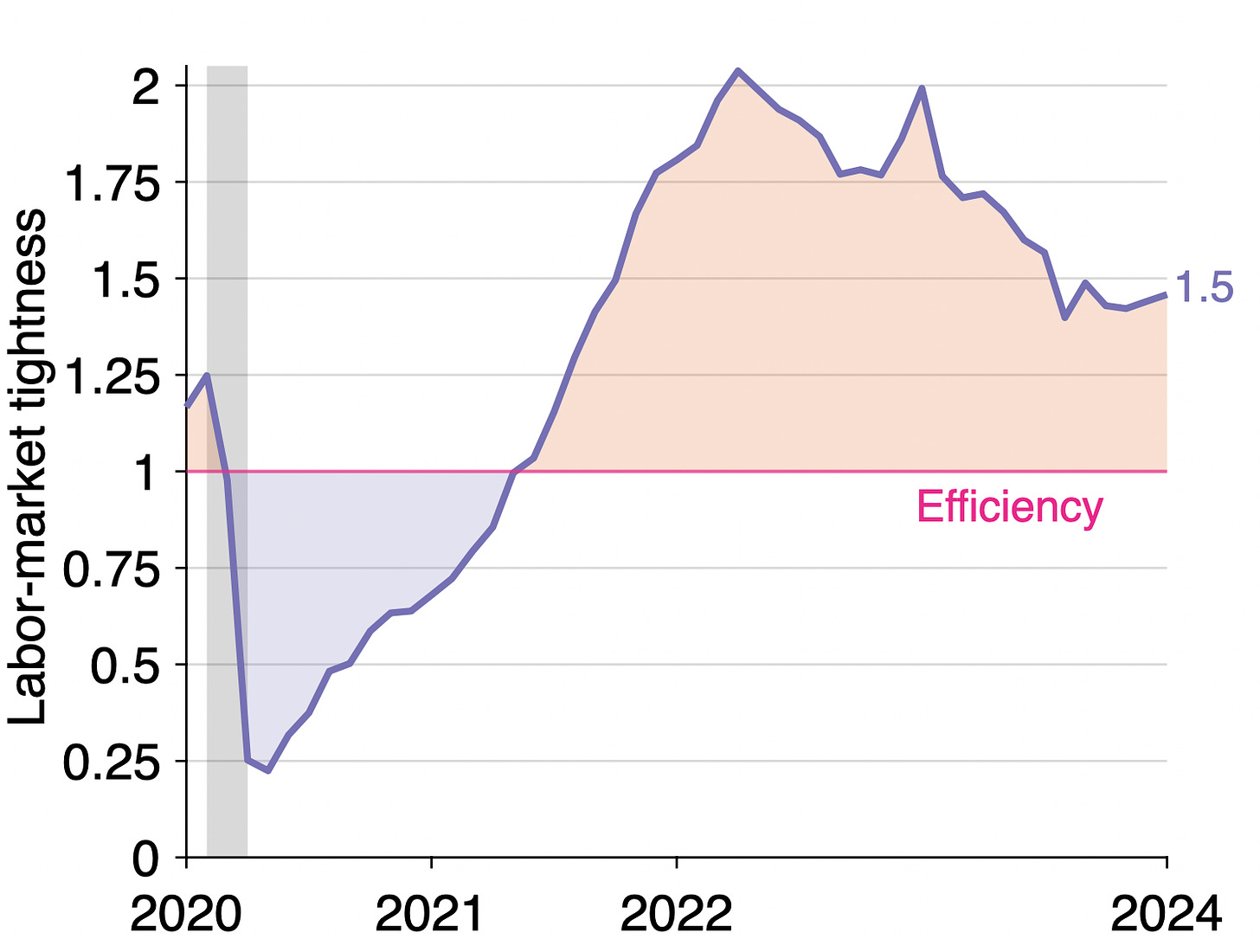
• Labor-market tightness: v/u = 5.4/3.7 = 1.5. This is up from 1.4 in December.

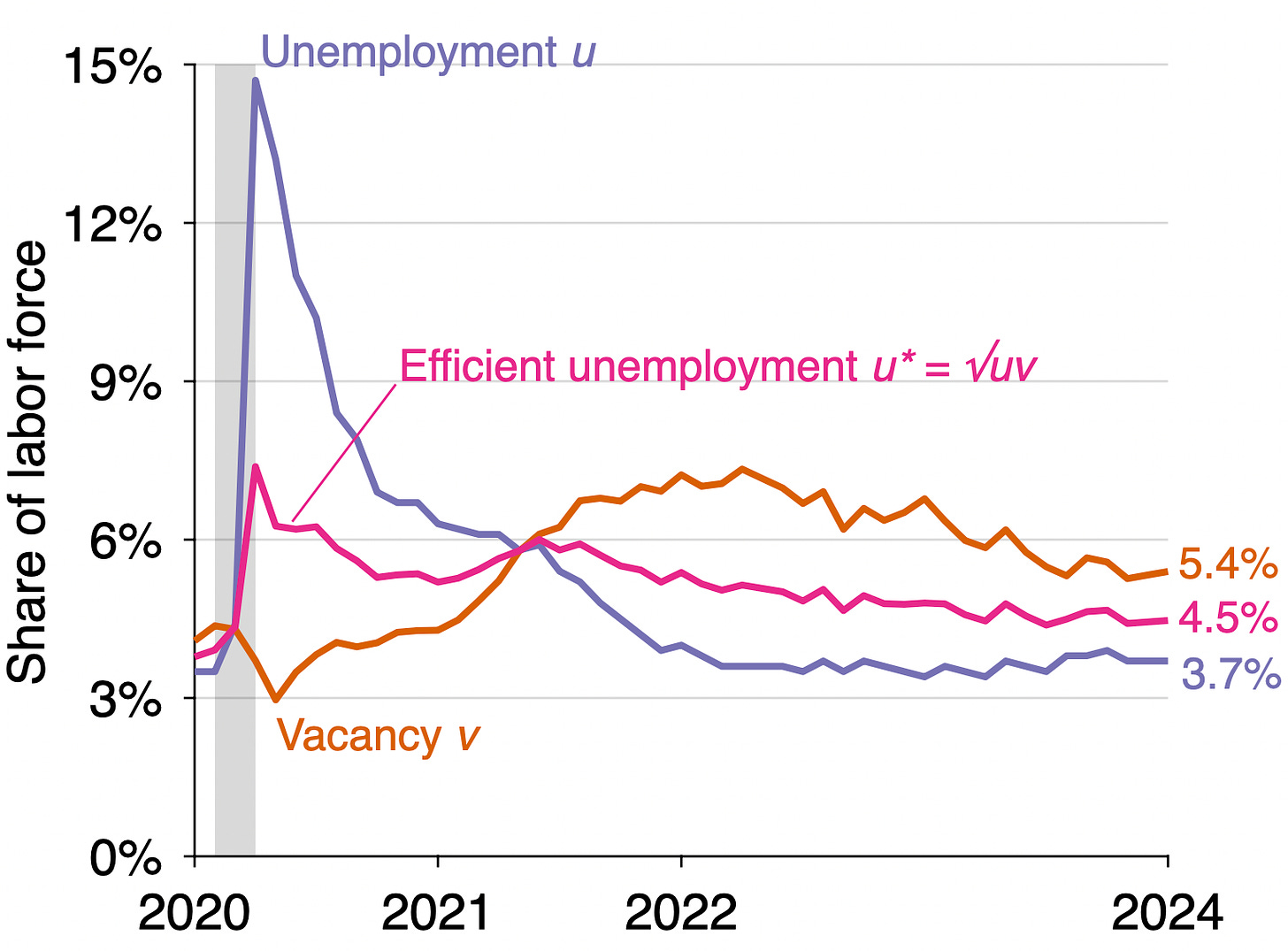
• Efficient unemployment rate: u* = √uv = √(0.037 × 0.054) = 4.5%. This is up from 4.4% in December.

• Unemployment gap: u – u* = 0.037 – 0.045 = –0.8pp. The gap has widened from –0.07pp in December.

Background for readers just joining us

The construction of the unemployment rate and vacancy rate from data provided by the Bureau of Labor Statistics is detailed in a previous post. The formula u* = √uv for the efficient unemployment rate is derived in a recent paper by Emmanuel Saez and me. The formula implies that the labor market is efficient when there are as many unemployed workers as vacant jobs (u = v); inefficiently tight when there are fewer unemployed workers than vacant jobs (u < v); and inefficiently slack when there are more unemployed workers than vacant jobs (u > v).

Is the US labor market is too tight or too slack?

Since the vacancy rate is above the unemployment rate (5.4% > 3.7%), the US labor market remains inefficiently tight. This means that the labor market is above full employment: the labor market is so hot that an excessive amount of labor is devoted to recruiting and hiring instead of producing. The labor market has been inefficiently tight since May 2021:

We can also see that the US labor market is inefficiently tight by looking at labor-market tightness v/u. Tightness remains above unity (1.5 > 1)—in fact it rebounded slightly in January—which indicates that the labor market is inefficiently hot:

How far is unemployment from its efficient rate?

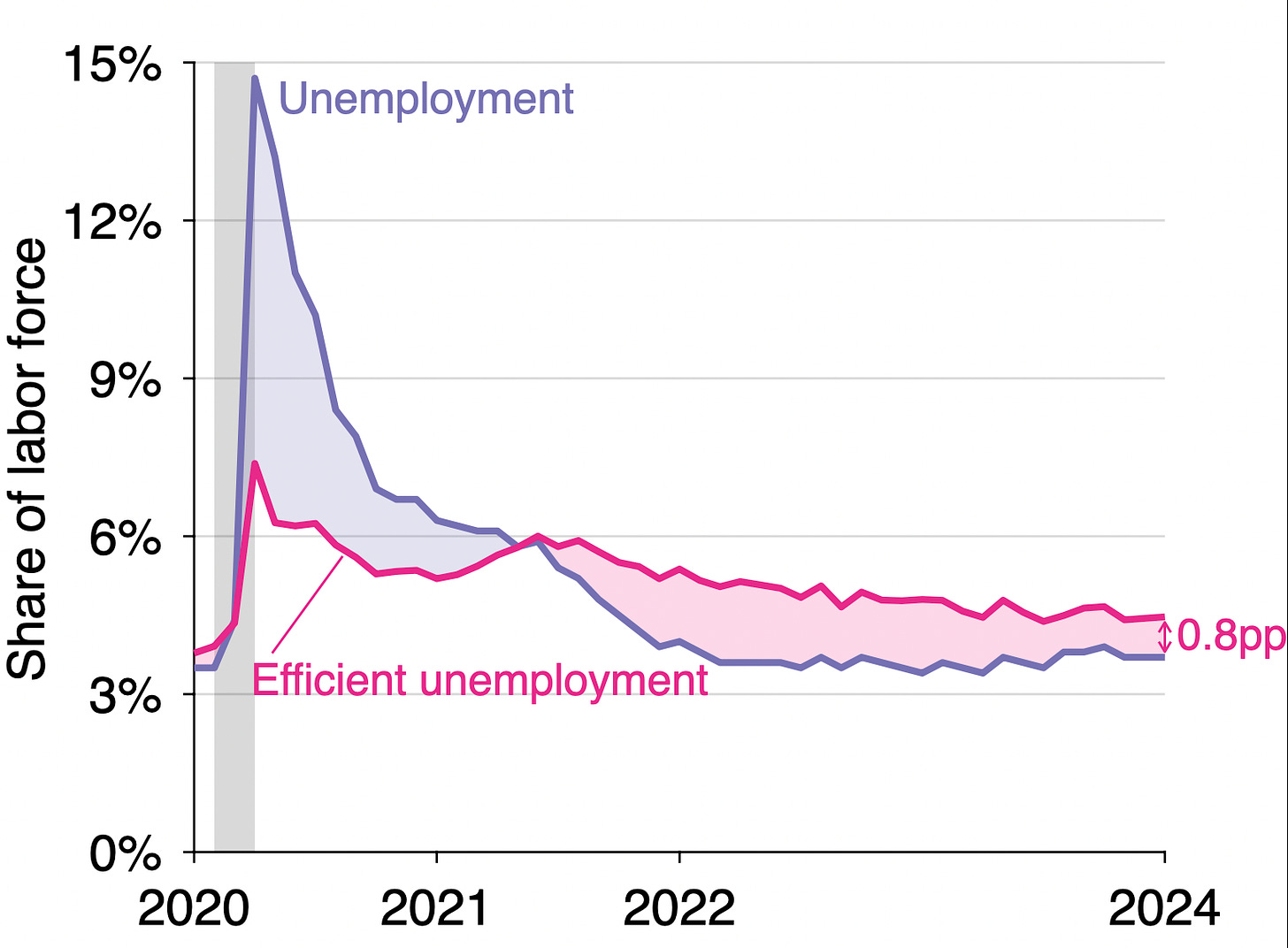
Since the labor market is inefficiently tight, the actual unemployment rate remains below the efficient unemployment rate. The graph below illustrates the construction of the efficient unemployment rate:

The efficient unemployment rate is 0.8 percentage point above the actual unemployment rate (u* = 4.5% while u = 3.7%). This negative unemployment gap is another manifestation of an inefficiently tight labor market. Below is the evolution of the unemployment gap over the course of the pandemic. The unemployment gap has been negative (u* > u) since the middle of 2021:

Implications for monetary policy

Full-employment mandate

One of the mandates of monetary policy is to maintain the economy at full employment. Although the law does not specify what full employment is, it is natural to interpret it as a socially efficient level of unemployment. Thus one of the goals of monetary policy is to maintain unemployment at its efficient rate, u*.

Unemployment is currently below its efficient rate, so a static reasoning suggests that monetary policy should continue to tighten to cool aggregate demand and labor demand. The monetary multiplier is around 0.5: when the Fed raises the federal funds rate by 1 percentage point, the unemployment rate increases by 0.5 percentage point. The current unemployment gap is -0.8pp, so statically it seems that the Fed should raise the fed funds rate by an additional 0.8/0.5 = 1.6pp to eliminate the gap.

However, monetary policy only affects the economy slowly. It takes about 1.5 years for a change in the fed funds rate to take effect fully. In the past two years, the Fed has raised the fed funds rate by 5.25pp. Only a fraction of that increase has taken effect. The rest might be enough to bring the unemployment rate to its efficient level. Indeed, given a monetary multiplier of 0.5, we would expect the total increase in interest rates to raise the unemployment rate by 5.25 × 0.5 = 2.6pp.

The unemployment gap in mid-2022, when the Fed started tightening, was -1.6pp. Everything else equal, we would expect the unemployment gap to turn positive once monetary policy has been fully absorbed, at -1.6 + 2.6 = 1.0pp. Under this basic scenario, the current monetary tightening would be sufficient to bring the labor market to efficiency—and maybe even to the inefficient slack territory.

Price-stability mandate and divine coincidence

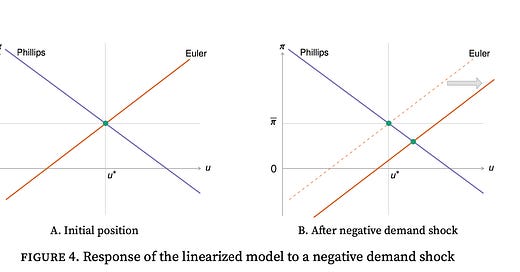
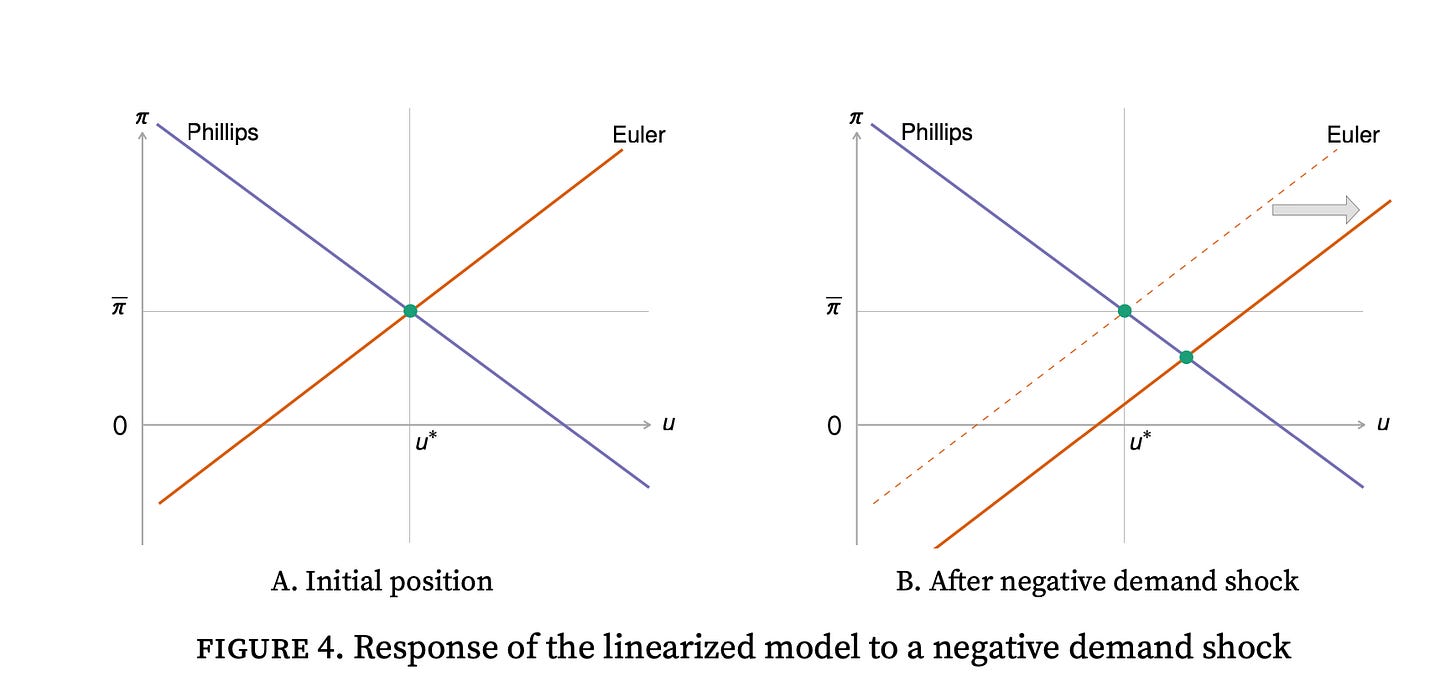
Of course, this recommendation does not take into account inflation. This is purely to improve the allocation of labor between producing, recruiting, and jobseeking. However, in the first draft of a new paper, Emmanuel Saez and I find that in a macroeconomic model with unemployment, under standard pricing assumptions (directed search with quadratic price-adjustment costs), the Phillips curve is such that the divine coincidence prevails. That is, the Phillips curve ensures that whenever the economy is at full employment, inflation is on target, at 2%. The diagram below illustrates the divine coincidence in our model (panel A) as well as the response to a tightening of monetary policy (panel B):

In such a model, the Fed’s two mandates coincide. So by keeping the economy at full employment, the Fed also maintains inflation at 2%.

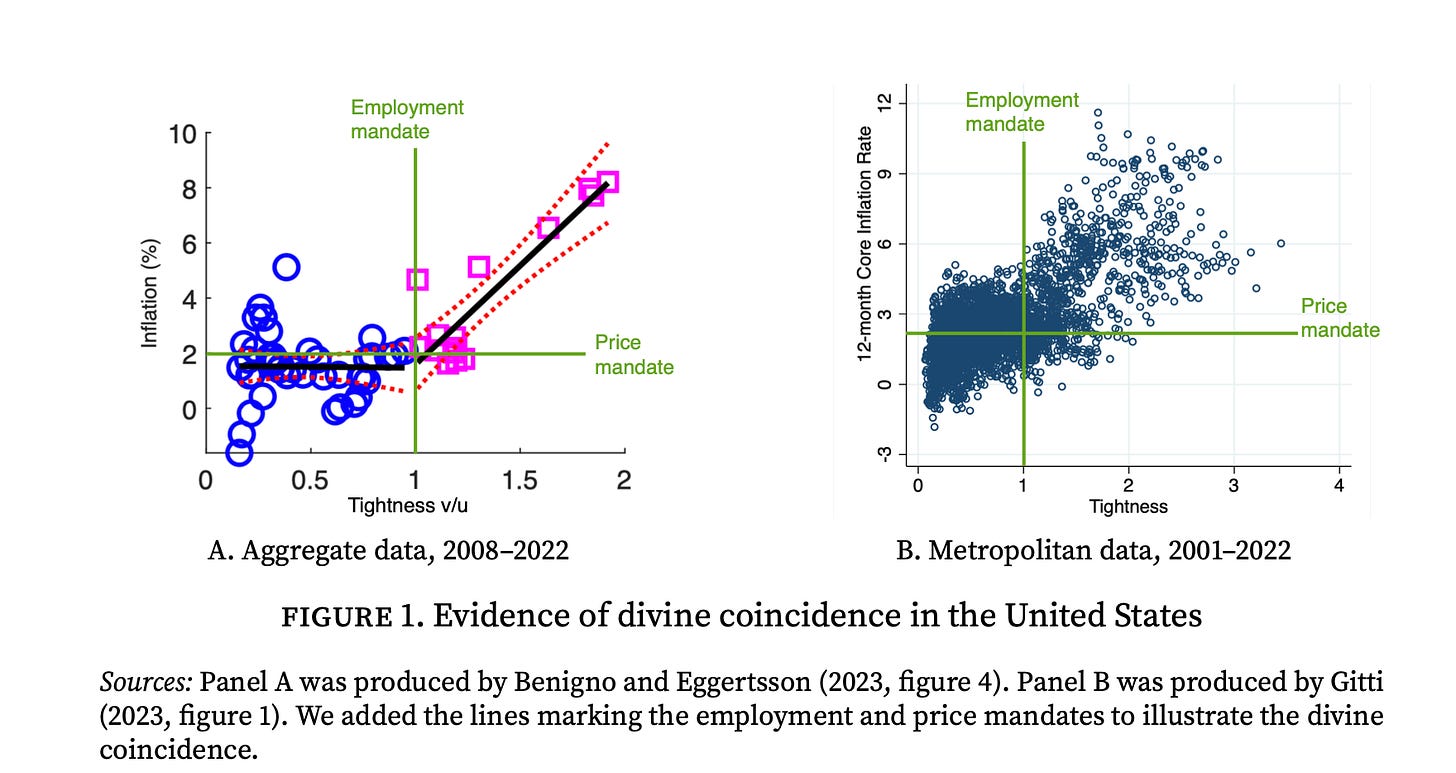
How realistic is the property of divine coincidence? Traditionally monetary economists thought the property was fairly unrealistic. However, in recent work, Pierpaolo Benigno and Gauti Eggertsson and Giulia Gitti find that the divine coincidence is clearly visible in US data. The figure below, based on their work, displays the divine coincidence in aggregate US data (panel A) and metropolitan US data (panel B):

So, targeting the efficient unemployment rate u* = √uv might be the only thing that the Fed should worry about, and they might have done enough to reach it.