How Can We Deal with P-hacking?
A simple theory of hypothesis testing with p-hacking provides critical values robust to p-hacking.
P-hacking occurs when scientists engage in various behaviors that increase their chances of reporting statistically significant results. Typical p-hacking practices include:
Running many small-sample experiments rather than one large-sample experiment
Reporting studies with significant results but suppressing studies with insignificant results
Collecting data until a significant result is obtained
Dropping inconvenient observations or outcomes from a study
Searching for statistical specifications that produce significant results
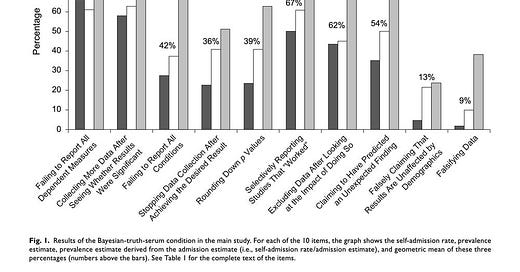
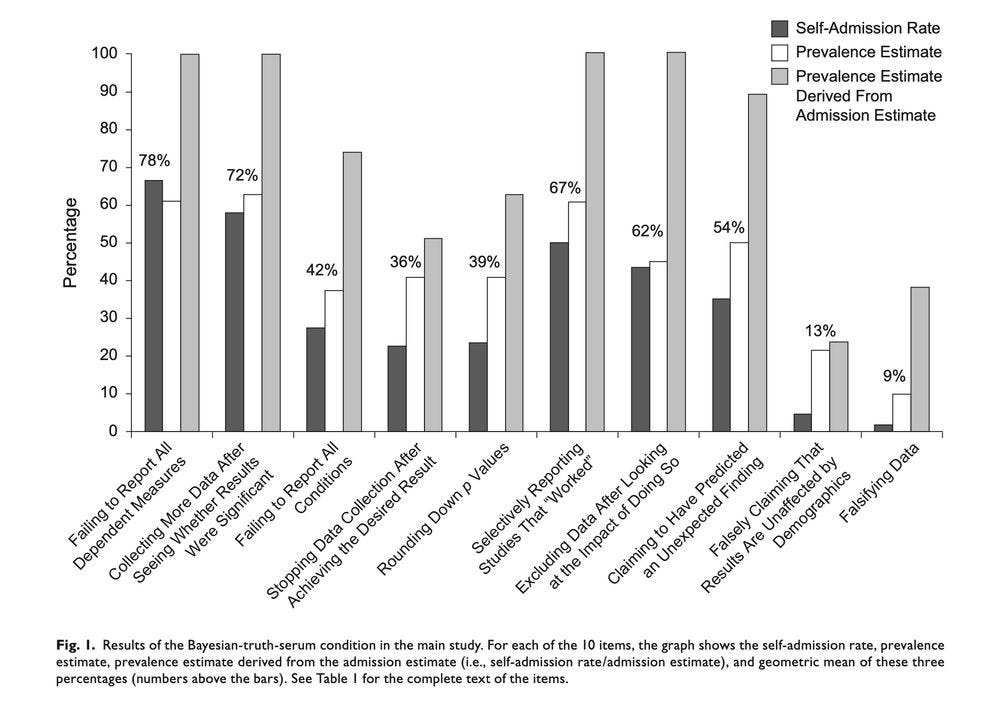
P-hacking is absent from hypothesis-testing theory, but it is ubiquitous in reality. In fact, p-hacking is so prevalent that scientists openly admit that they p-hack:
It is not surprising that p-hacking is so prevalent because scientists have large incentives to p-hack. This is because scientific journals prefer publishing significant results. But p-hacking threatens scientific progress. It leads to excessive rejection of established paradigms and to the unwarranted adoption of new paradigms. One manifestation of uncontrolled p-hacking is the replication crisis in science.
In a paper recently accepted at REStat, Adam McCloskey and I work on the p-hacking problem. Our main contribution is to derive critical values that correct the inflated type 1 error rate (false positive rate) caused by p-hacking. The paper will come out in print in 2026; meanwhile the final version is online at pascalmichaillat.org/12/.
In the paper, we build a model of hypothesis testing that accounts for p-hacking and derive critical values robust to p-hacking from it. From the model, we derive critical values such that, if they are used to determine significance, and if p-hacking adjusts to the new significance standards, spurious significant results do not occur more often than intended.
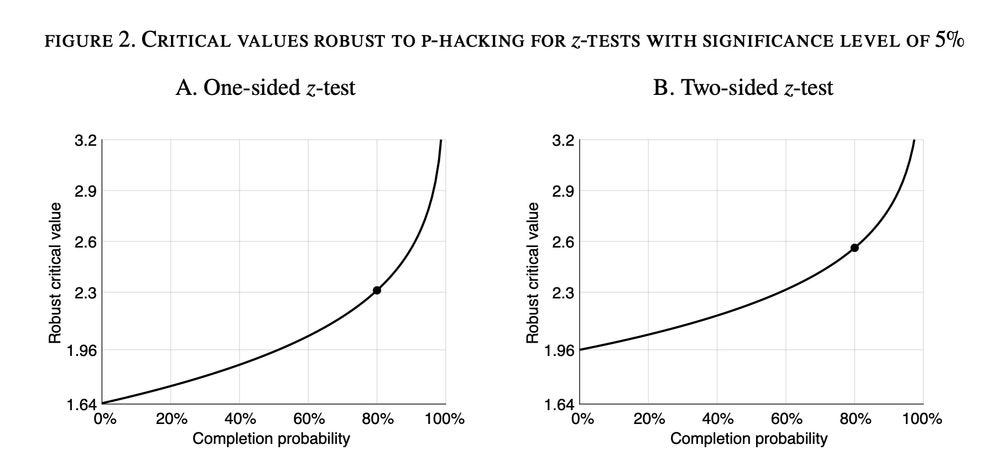
Because of p-hacking, robust critical values are larger than classical critical values. In the model calibrated to medical science, the robust critical value is the classical critical value for the same test statistic but with one fifth of the significance level.
A common hypothesis test is a z-test with significance level of 5%. Under the medical science calibration, the robust critical values are 2.33 if the test is one-sided & 2.58 if the test is two-sided—somewhat higher than the classical critical values of 1.64 & 1.96.
We also find that robust critical values are higher when it is easier to p-hack (for instance, when it is easier to complete experiments). This means that ideally critical values should be higher for teams with more resources & higher in fields in which running experiments is easier. Critical values should also be raised when technological progress makes p-hacking easier. An example of such progress is the advent of online surveys and experiments in the social sciences, which have simplified the task of collecting data.
We examine the sensitivity of the robust critical values to the calibration of the probability to complete an experiment. This probability is the key parameter of the model; its baseline calibration is 80%. We find that robust critical values are not too sensitive to it:
Our analysis provides a theoretical underpinning for the proposals to reduce the significance levels used in science—such as the proposal to reduce the default significance level from 5% to 0.5% by Dan Benjamin and many others in Nature Human Behavior. The tenfold reduction in the significance level that they propose is a more aggressive response to p-hacking than the fivefold reduction obtained in our baseline calibration. But it would be appropriate for an experiment completion probability of 90%.
Finally, our robust critical values offer an alternative to pre-analysis plans for dealing with p-hacking. An advantage of the robust critical values over pre-analysis plans is that they do not impede the process of scientific exploration & discovery.